2024Í¿ÇÒÓ ÍÊÒÍñýӣͥÍÏÿ¥233Ó§Ì ÀÒÓ ð¡Íý¡ÍÓ£ÍÊÏÍÛÑÌÇÓð¤ÒÓ Ì¯ÍÙÎÕ¨ÕÂÕÕƒÒÓ¿ÿ¥ðƒÍÊÏÍÛÑÍÙÎð¿ ÿ¥Í£¤ÒÛÛÌÑÒÐ
Í₤ÍÓΣÓ̓ÛÍÌ¿Ó´Ðէ̘À̓ÛÍÌ¿Ó´Ðէ̘Àð¡ÕÑÓ¤¢ÌÏ̓ÛÍÌ¿Ó´ÐÕէ̘Àð¡ÕÑÓ¤¢ÌÏ̓ÛÍÌ¿Ó´Ð
Í₤ÍÓΣÓ̓ÛÍÌ¿Ó´ÿ¥
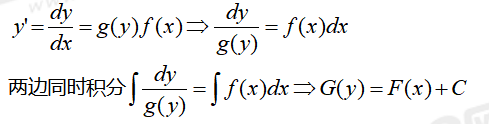
է̘À̓ÛÍÌ¿Ó´ÿ¥
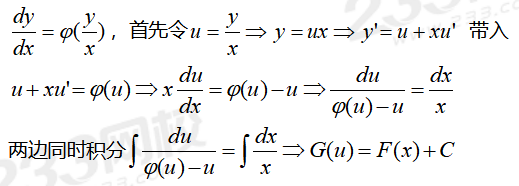
է̘Àð¡ÕÑÓ¤¢ÌÏ̓ÛÍÌ¿Ó´ÿ¥
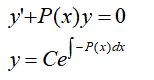
է̘Àð¡ÕÑÓ¤¢ÌÏ̓ÛÍÌ¿Ó´ÿ¥
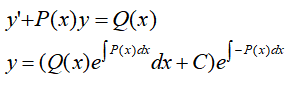
ÓÇÒÏÍÌ Ó°£ð¡ð¤ÕÓÏ₤Íð¡ÌÍÌ ð¡Óð¤ÕÓÏ₤Íÿ¥ÓÇÒÏÍÌ Ó°£ð¡ð¤ÕÓÏ₤ÍÍð¡ÊÓÏÿ¥ð¡ÓÏÌ₤Ì₤XÍÐð¡ÓÏÌ₤YÍÐ
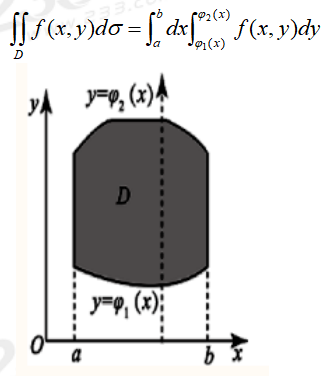
XÍÿ¥ÒÛƒÓÏ₤ÍͤÍDÿ¥aãÊxãÊbÿ¥ü1(x)ãÊyãÊü2(x)ÿ¥ÍÎ̓ÌÓʤÿ¥ü1(x)ÿ¥ü2(x)ʹͤÕÇ[a, b]ð¡Ò¢Ó£ÙÐ
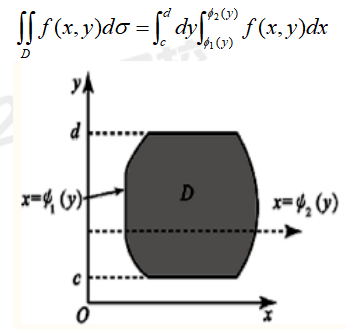
YÍÿ¥ÒÛƒÓÏ₤ÍͤÍDÿ¥cãÊyãÊdÿ¥ü1(y)ãÊyãÊü2(y)ÿ¥ÍÎ̓ÌÓʤÿ¥ü1(x)ÿ¥ü2(x)ʹͤÕÇ[c, d]ð¡Ò¢Ó£ÙÐ
ÌÍÌ ð¡Óð¤ÕÓÏ₤Íÿ¥ÓÝÌÍÌ ÍÌÂÿ¥ÒÛƒx=rcosö¡ÿ¥y=rsinö¡ÿ¥ÒËÓÏ₤ÍͤÍDÿ¥Íÿ¥

ã ÍÎÌÓÏ₤ÍͤÍDÍ °ð¤xÒ§ÇÍ₤¿Óϯÿ¥Í

Í Ñð¡ÙD1ð¡¤DÓð¡ÍÍ¿°ÕÂÓÕ´ÍÐ
ãÀÍÎÌÓÏ₤ÍͤÍDÍ °ð¤yÒ§ÇÍ₤¿Óϯÿ¥Í

Í Ñð¡ÙD2ð¡¤DÒ§§Í°ÍÍ¿°ÕÂÓÕ´Í
ãÂÍÎÌÓÏ₤ÍͤÍDÍ °ð¤y=xÍ₤¿Óϯÿ¥Í
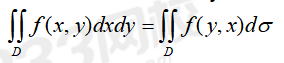
ãÈÍÎÌÓÏ₤ÍͤÍD1ÿ¥D2Í °ð¤ÓÇÓ¤¢y=xÍ₤¿Óϯÿ¥Í
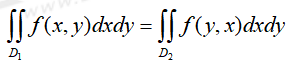
ãÊÍÎÌÓÏ₤ÍͤÍDÍ °ð¤ÓÇÓ¤¢y=xÍ₤¿Óϯÿ¥Í
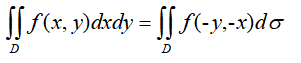
ð¤Í ̯ͧf(x,y)ÌÍ¥ÍÙÍ´ÓÍ¢ ÒÎÌÀð£Ñÿ¥Òۃ̯ͧf(x,y)Í´Ó¿(x0,y0)ÍÊÍÍ₤¥Ì¯ÍÙÍ´ÿ¥ð¡Í´Ó¿(x0,y0)ÍÊÍ̓ÌÍ¥ÿ¥Íf'x(x0,y0)=0, f'y(x0,y0)=0Ð
ð¤Í ̯ͧÌÍ¥ÓÌÝÒÏÈÌ¿Ì°ÿ¥Í f(x,y)Í₤¿xÿ¥yÍͨÌÝͤÍÍ₤¥Í¿Ñð£Êð£ð£˜ÓÙð¤0
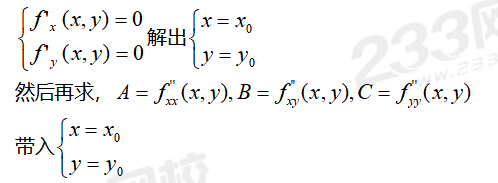
ÿ¥1ÿ¥AC-B2ÿ¥0ÌÑÿ¥ÌÍ¥ÍÙÍ´ÿ¥ð¡Í§Aÿ¥0ÌÑÌÌÍÊÏÍ¥ÿ¥Í§Aÿ¥0ÌÑÌÌͯͥÐ
ÿ¥2ÿ¥AC-B2ÿ¥0ÌÑÿ¥ÌÍ¥ð¡ÍÙÍ´Ð
Ó´ÌÌ ¥ÌÌËÌ°ÿ¥
ÕÎÍ ÿ¥ÌÕ ÌÌ ¥ÌÌË̯ͧF(x,y)=f(x,y)+ö£ü(x,y)ÿ¥

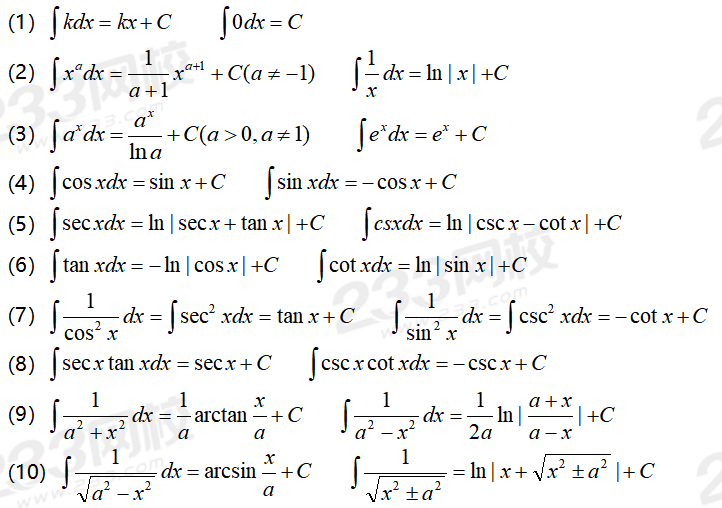

ÌÏÒÇ´1 f(x)ʹͤÕÇ[a, b]ð¡Í₤ÓÏ₤ÓÍ¢ ÒÎÌÀð£ÑÌ₤f(x)ʹͤÕÇ[a, b]ð¡ÌÓÐ
ÌÏÒÇ´2 f(x)Í₤ÓÏ₤ÓÍ ÍÌÀð£ÑÌÍÎð¡ð¡ð¡ˆÿ¥
ÿ¥iÿ¥ÒËf(x)ʹͤÕÇ[a, b]ð¡Ò¢Ó£Ùÿ¥Íf(x)Í´[a, b]ð¡Í₤ÓÏ₤
ÿ¥iiÿ¥ÒËf(x)ʹͤÕÇ[a, b]ð¡ÌÓÿ¥ÕÊÌÕð¡ˆÕÇÌÙÓ¿ÍÊ̯ͧҢӣÙÿ¥Íf(x)Í´[a, b]ð¡Í₤ÓÏ₤
ÿ¥iiiÿ¥ÒËf(x)ʹͤÕÇ[a, b]ð¡ÍÒ¯ÿ¥Íf(x)Í´[a, b]ð¡Í₤ÓÏ₤Ð
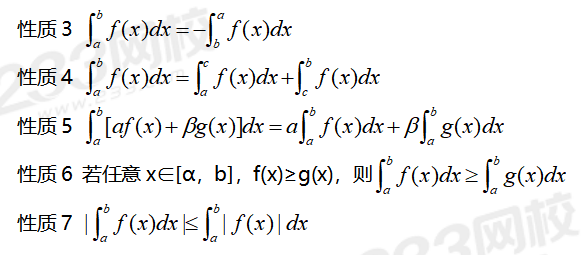
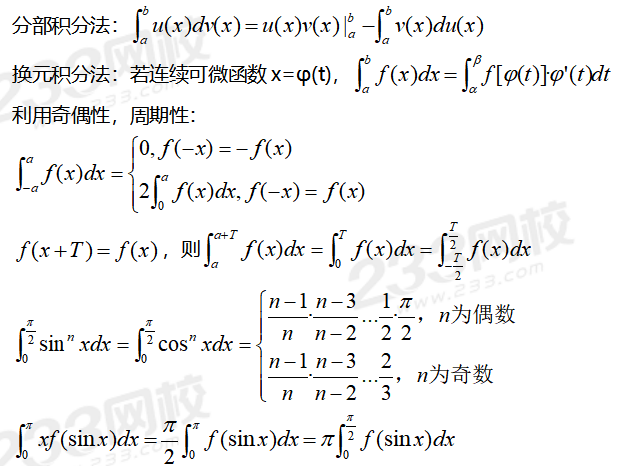
ÒÇ¿Õˋ˜ÍÛÓÿ¥Òۃ̯ͧy=f(x)Í´Ó¿x0ÓÌÕÂÍU(x0)Í ÌÍÛð¿ÿ¥ð¡Í´x0ÍÊÍ₤Í₤¥ÿ¥ÒËÍ₤¿ð££ð¡xãU(x0)ÿ¥Ìf(x)ãÊf(x0)Ìf(x)ãËf(x0)ÿ¥Ífã(x0)=0Ð
ӧͯÍÛÓÿ¥Òۃ̯ͧy=f(x)Í´ÕÙͤÕÇ[aÿ¥b]ð¡Ò¢Ó£Ùÿ¥Í´Í¥Í¤ÕÇÿ¥aÿ¥bÿ¥Í Í₤Í₤¥ÿ¥ð¡f(a)=f(b)ÿ¥ÍҰͯÍÙÍ´ð¡Ó¿öƒãÿ¥aÿ¥bÿ¥ÿ¥ð§¢Íƒfã(öƒ)=0Ð
ÌÌ ¥ÌÌËð¡ÙÍ¥ÍÛÓÿ¥Òۃ̯ͧy=f(x)Í´ÕÙͤÕÇ[aÿ¥b]ð¡Ò¢Ó£Ùÿ¥Í´Í¥Í¤ÕÇÿ¥aÿ¥bÿ¥Í Í₤Í₤¥ÿ¥ÍҰͯÍÙÍ´ð¡Ó¿öƒãÿ¥aÿ¥bÿ¥ÿ¥ð§¢Íƒf(b)-f(a)=fã(öƒ)(b-a)Ð
Ì₤ÒË¢ð¡ÙÍ¥ÍÛÓÿ¥Òۃ̯ͧf(x)ÿ¥g(x)Í´ÕÙͤÕÇ[aÿ¥b]ð¡Ò¢Ó£Ùÿ¥Í´Í¥Í¤ÕÇÿ¥aÿ¥bÿ¥Í
Í₤Í₤¥ÿ¥ð¡Í₤¿ð££ð¡xãÿ¥aÿ¥bÿ¥ÿ¥gã(x)ã 0ÿ¥ÍҰͯÍÙÍ´ð¡Ó¿öƒãÿ¥aÿ¥bÿ¥ÿ¥ð§¢Íƒ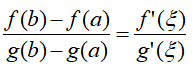 Ð
Ð
ÕÑÓ¿ÍÛÓÿ¥Òۃ̯ͧf(x)Í´ÕÙͤÕÇ[a,b]ð¡Ò¢Ó£Ùÿ¥ð¡f(a)ð¡ f(b)Í¥Íñÿ¥Í°f(a)û f(b)<0ÿ¥ÿ¥ÕÈð¿Í´Í¥Í¤ÕÇÿ¥a,bÿ¥Í ҰͯÌ̯ͧf(x)Óð¡ð¡ˆÕÑÓ¿ÿ¥Í°Ò°Í¯Ìð¡Ó¿öƒÿ¥a<öƒ<bÿ¥ð§¢f(öƒ)=0Ð
ð£Í¥ÍÛÓÿ¥Òۃ̯ͧf(x)Í´ÕÙͤÕÇ[a,b]ð¡Ò¢Ó£Ùÿ¥ð¡Í´Ò¢Í¤ÕÇÓÓ¨₤Ó¿Íð¡ÍÓ̯ͧͥÿ¥f(a)=AÍf(b)=Bÿ¥ÕÈð¿ÿ¥Í₤¿ð¤Að¡Bð¿ÕÇÓð££Ìð¡ð¡ˆÌ¯Cÿ¥Í´Í¥Í¤ÕÇ(a,b)Í Ò°Í¯Ìð¡Ó¿öƒÿ¥ð§¢Íƒf(öƒ)=C (a<öƒ<b)Ð
Ì°¯ÍÍÛÓÿ¥Òۃ̯ͧy=f(x)Í´ÕÙͤÕÇ[aÿ¥b]ð¡ÌÒ¢Ó£ÙÓnÕÑÍ̯ÿ¥Í´Í¥Í¤ÕÇÿ¥aÿ¥bÿ¥Í Ìn+1ÕÑÍ̯ÿ¥ÍÍ₤¿ð££ð¡xãÿ¥aÿ¥bÿ¥ÿ¥Ì

Ó˜˜ð¡ÓÏÍÊÍÛÌ¿Ì°ÿ¥Òۃ̯ͧy=f(x)Í´x0ÍÊÒ¢Ó£Ùÿ¥ð¡Í´x0ÓÌͣ͢ÕÂÍUÿ¥x0ÿ¥öÇÿ¥Í Í₤Í₤¥
ÿ¥1ÿ¥ÒËͧxãÿ¥x0-öÇÿ¥x0ÿ¥ÌÑÿ¥fã(x)>0ÿ¥Òͧxãÿ¥x0ÿ¥x0+öÇÿ¥ÌÑÿ¥fã(x)<0ÿ¥Íf(x)Í´x0ÍÊÍ̓ÌÍÊÏÍ¥.
ÿ¥2ÿ¥ÒËͧxãÿ¥x0-öÇÿ¥x0ÿ¥ÌÑÿ¥fã(x)<0ÿ¥Òͧxãÿ¥x0ÿ¥x0+öÇÿ¥ÌÑÿ¥fã(x)>0ÿ¥Íf(x)Í´x0ÍÊÍ̓Ìͯͥ.
ÿ¥3ÿ¥ÒËͧxãUÿ¥x0ÿ¥öÇÿ¥ÌÑÿ¥fã(x)Ó˜ÎÍñð¢Ìð¡Íÿ¥Íf(x)Í´x0ÍÊÌ ÌÍ¥.
Ó˜˜ð¤ÓÏÍÊÍÛÌ¿Ì°ÿ¥Òۃ̯ͧy=f(x)Í´x0ÍÊÌð¤ÕÑÍ₤¥Ì¯ð¡fã(x0)=0ÿ¥fã(x)ã 0ÿ¥Í
ÿ¥1ÿ¥Í§fã(x)<0ÌÑÿ¥Í§Ì¯y=f(x)Í´x0ÍÊÍ̓ÌÍÊÏÍ¥
ÿ¥2ÿ¥Í§fã(x)>0ÌÑÿ¥Í§Ì¯y=f(x)Í´x0ÍÊÍ̓Ìͯͥ
Òۃ̯ͧy=f(x)Í´[aÿ¥b]ð¡Ò¢Ó£Ùÿ¥Í´ÿ¥aÿ¥bÿ¥Í Ìð¡ÕÑÍð¤ÕÑÍ₤¥Ì¯ÿ¥Í
ÿ¥1ÿ¥ÒËÍ´ÿ¥aÿ¥bÿ¥Í fã(x)>0ÿ¥Í̯ͧy=f(x)Í´[aÿ¥b]ð¡Ó̓ͧÂÌ₤Í¿Ó
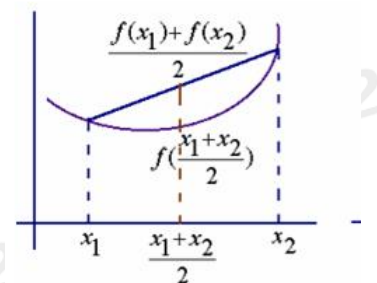
ÿ¥2ÿ¥ÒËÍ´ÿ¥aÿ¥bÿ¥Í fã(x)<0ÿ¥Í̯ͧy=f(x)Í´[aÿ¥b]ð¡Ó̓ͧÂÌ₤Í¡Ó
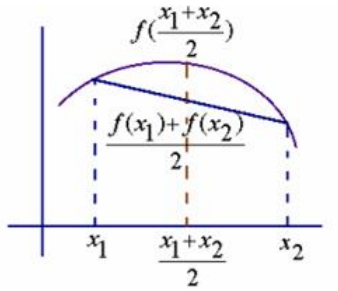

Í¡¡ÒÏÓÍÓÙ̯ͧÓnÕÑÍ₤¥Ì¯Í ˜Í¥ÿ¥



Ì¡ˋÕδÌÓʤÿ¥ÌÓ¨ ÓÝð§Ò 233Ó§Ì À-chenjingÓ˜Ó¨Íð§ÍÛÌÿ¥ÌˆÓ£Òð§Ìð¤¤ÍÌÓÎÌÙÂÒ§˜Ò§§Ð
