و»،هˆ†ن¸؛150هˆ†ï¼Œè€ƒè¯•و—¶é—´ن¸؛180هˆ†é’ںم€‚ç”é¢کو–¹ه¼ڈن¸؛é—هچ·م€پ笔试م€‚
试هچ·ç»“و„ï¼ڑ
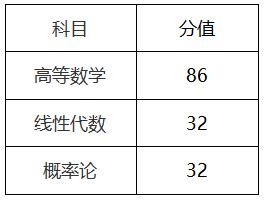
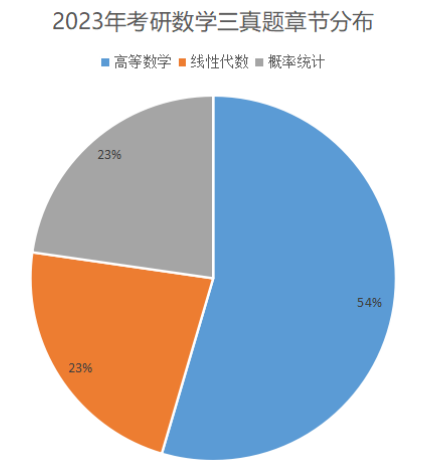
第ن¸€éƒ¨هˆ† é«کç‰و•°ه¦
| ç« èٹ‚ | 考و ¸çں¥è¯†ç‚¹ | ه‡؛é¢کو€§è´¨ | هˆ†ه€¼ |
| 第ن¸€ç« ه‡½و•°م€پوپé™گم€پè؟ç» | وپé™گو±‚解 | ه،«ç©؛é¢کT11 | 5 |
| 第ن؛Œç« ن¸€ه…ƒه‡½و•°ه¾®هˆ†ه¦ | ه¾®هˆ†çڑ„ه؛”用م€پن¸ه€¼ه®ڑçگ† | 解ç”é¢کT17م€پ解ç”é¢کT20 | 24 |
| 第ن¸‰ç« ن¸€ه…ƒه‡½و•°ç§¯هˆ†ه¦ | هژںه‡½و•°م€پو—‹è½¬ن½“ | ه،«ç©؛é¢کT2م€پ解ç”é¢کT18 | 5 |
| 第ه››ç« ه¤ڑه…ƒه‡½و•°ه¾®هˆ†ه¦ | هپڈه¯¼و•°çڑ„ه®ڑن¹‰م€په¤ڑه…ƒه‡½و•°çڑ„ه€¼ | 选و‹©é¢کT1م€په،«ç©؛é¢کT12 | 10 |
| 第ن؛”ç« ن؛Œé‡چ积هˆ† | ن؛Œé‡چ积هˆ†è®،ç®— | 解ç”é¢کT19 | 12 |
| 第ه…ç« ه¤ڑه…ƒه‡½و•°ç§¯هˆ†ه¦ | هپڈه¯¼و•°çڑ„ه®ڑن¹‰م€په¤ڑه…ƒه‡½و•°çڑ„ه€¼ | 选و‹©é¢کT1م€په،«ç©؛é¢کT12 | 10 |
| 第ن¸ƒç« و— ç©·ç؛§و•° | و”¶و•›çڑ„هˆ¤هˆ«م€په’Œه‡½و•° | 选و‹©é¢کT4م€په،«ç©؛é¢کT13 | 10 |
| 第ه…«ç« ه¸¸ه¾®هˆ†و–¹ç¨‹ | ه¾®هˆ†و–¹ç¨‹çڑ„解 | 选و‹©é¢کT3م€په،«ç©؛é¢کT14 | 10 |
| و€»هˆ† | 86 | ||
第ن؛Œéƒ¨هˆ† ç؛؟و€§ن»£و•°
| ç« èٹ‚ | 考و ¸çں¥è¯†ç‚¹ | ه‡؛é¢کو€§è´¨ | هˆ†ه€¼ |
| 第ن¸€ç« è،Œهˆ—ه¼ڈ | è،Œهˆ—ه¼ڈçڑ„è®،ç®— | ه،«ç©؛é¢کT15 | 5 |
| 第ن؛Œç« çں©éکµ | ن¼´éڑڈçں©éکµ | 选و‹©é¢کT5 | 5 |
| 第ن¸‰ç« هگ‘é‡ڈ | ç؛؟و€§è،¨ç¤؛ | 选و‹©é¢کT7 | 5 |
| 第ه››ç« ç؛؟و€§و–¹ç¨‹ç»„ | |||
| 第ن؛”ç« ç‰¹ه¾په€¼ن¸ژ特ه¾پهگ‘é‡ڈ | 相ن¼¼ه¯¹è§’هŒ– | 解ç”é¢کT21 | 12 |
| 第ه…ç« ن؛Œو¬،ه‹ | ن؛Œو¬،ه‹çڑ„规范ه‹ | 选و‹©é¢کT6 | 5 |
| و€»هˆ† | 32 | ||
第ن¸‰éƒ¨هˆ† و¦‚çژ‡è®؛
| ç« èٹ‚ | 考و ¸çں¥è¯†ç‚¹ | ه‡؛é¢کو€§è´¨ | هˆ†ه€¼ |
| 第ن¸€ç« éڑڈوœ؛ن؛‹ن»¶ه’Œو¦‚çژ‡ | 0 | ||
| 第ن؛Œç« éڑڈوœ؛هڈکé‡ڈهڈٹه…¶هˆ†ه¸ƒ | و¦‚çژ‡ه¯†ه؛¦çڑ„è®،ç®— | 解ç”é¢کT22 | 12 |
| 第ن¸‰ç« ه¤ڑç»´éڑڈوœ؛هڈکé‡ڈهڈٹه…¶هˆ†ه¸ƒ | |||
| 第ه››ç« éڑڈوœ؛هڈکé‡ڈçڑ„و•°ه—特ه¾پ | وœںوœ›çڑ„è®،ç®—م€پ相ه…³ç³»و•° | 选و‹©é¢کT8م€په،«ç©؛é¢کT16 | 10 |
| 第ن؛”ç« ه¤§و•°ه®ڑه¾‹ه’Œن¸ه؟ƒوپé™گه®ڑçگ† | |||
| 第ه…ç« و•°çگ†ç»ںè®،çڑ„هں؛وœ¬و¦‚ه؟µ | Fهˆ†ه¸ƒ | 选و‹©é¢کT9 | 5 |
| 第ن¸ƒç« هڈ‚و•°ن¼°è®، | و— هپڈن¼°è®، | 选و‹©é¢کT10 | 5 |
| 第ه…«ç« هپ‡è®¾و£€éھŒ | 0 | ||
| و€»هˆ† | 32 | ||
第ن¸€é¢کï¼ڑهˆ©ç”¨ه®ڑن¹‰و±‚هپڈه¯¼ï¼Œه¸¸è§„考é¢کم€‚
第ن؛Œé¢کï¼ڑو±‚هژںه‡½و•°ï¼Œو³¨و„ڈè؟ç»و€§è؟™ن¸€ن¸ھه°ڈ点هچ³هڈ¯م€‚
第ن¸‰é¢کï¼ڑ考وں¥ه¾®هˆ†و–¹ç¨‹çڑ„解,ن½†وک¯éœ€è¦پèپ”ç³»هˆ°ن؛Œو¬،و–¹ç¨‹è§£çڑ„هˆ¤ه®ڑه…¬ه¼ڈ,考وں¥éڑ¾ه؛¦ه¾ˆé«ک,ن¸چçگ†è§£ه¾®هˆ†و–¹ç¨‹è§£çڑ„ه‡ ç§چوƒ…ه†µï¼Œه°±ه®¹وک“é€ وˆگن¸چçگ†è§£ن»€ن¹ˆهڈ«وœ‰ç•Œم€‚
第ه››é¢کï¼ڑه¯¹ç؛§و•°هˆ¤هˆ«و³•çڑ„考وں¥ï¼Œه¸¸è§„考点م€‚
第ن؛”é¢کï¼ڑن¼´éڑڈçں©éکµçڑ„و±‚解,è؟™ن¸ھé¢کوœ‰ن¸€ه®ڑéڑ¾ه؛¦ï¼Œو²،وœ‰è؟›è،Œè؟‡ç±»ن¼¼è®ç»ƒن¼ڑèٹ±è´¹ن¸چه°‘و—¶é—´ï¼Œهœ¨è®°ن½ڈن¼´éڑڈçں©éکµه…¬ه¼ڈçڑ„ه‰چوڈگن¸‹ï¼Œç„¶هگژه¸¦ه…¥è®،ç®—م€‚
第ه…é¢کï¼ڑن؛Œو¬،ه‹çڑ„考وں¥ن¹ںوک¯ه¸¸è€ƒç‚¹ï¼Œن½†وک¯è؟™ن¸ھ规范و€§çڑ„è®،算,ن¸چ能直观çڑ„é€ڑè؟‡و€§è´¨و±‚解,需è¦پو‹†ه¼€è®،算,هں؛ç،€è¦پ牢ه›؛,è¦پçگ†è§£è€ƒè¯•è€ƒوں¥ن½ çڑ„وک¯ه“ھن¸ھ点م€‚
第ن¸ƒé¢کï¼ڑه…¶ه®وک¯ن¸€ن¸ھه¤§é¢کو”¹ç¼–è؟‡و¥çڑ„,ه°±وک¯ç؛؟و€§ç›¸ه…³çڑ„解çڑ„çگ†è§£ï¼Œوœ‰ن¸€ه®ڑéڑ¾ه؛¦م€‚
第ه…«é¢کï¼ڑéڑڈوœ؛هڈکé‡ڈçڑ„وœںوœ›è®،算,首ه…ˆéœ€è¦پهˆ¤ه®ڑç»ه¯¹ه€¼ه†…çڑ„ه‡½و•°هˆ†ه¸ƒï¼Œه†چè؟›è،Œè®،ç®—م€‚
第ن¹é¢کï¼ڑFهˆ†ه¸ƒçڑ„هˆ¤و–,考وں¥éڑڈوœ؛و ·وœ¬çڑ„و¦‚ه؟µم€‚
第هچپé¢کï¼ڑه¸¸è§„考é¢ک,و— هپڈن¼°è®،م€‚
考وں¥ن¸€ن¸ھوپé™گم€پن¸€ن¸ھه¤ڑه…ƒه‡½و•°م€پن¸€ن¸ھو— ç©·ç؛§و•°çڑ„ه’Œه‡½و•°م€پن¸€ن¸ھه¾®هˆ†و–¹ç¨‹çڑ„解م€پè،Œهˆ—ه¼ڈçڑ„è®،ç®—ه’Œç›¸ه…³ç³»و•°ï¼Œéƒ½و¯”较ه¸¸è§„,çگ†è§£çں¥è¯†ç‚¹ï¼Œè®°ه؟†ه…¬ه¼ڈهچ³هڈ¯ç”é¢ک,éڑ¾ه؛¦éƒ½ن¸چه¤§م€‚
第ن¸€é¢ک考وں¥ه¯¼و•°çڑ„ه؛”用,第ن؛Œé¢کو±‚و—‹è½¬ن½“ن½“积,第ن¸‰é¢کè®،ç®—ن؛Œé‡چ积هˆ†ï¼Œç¬¬ه››é¢که¾®هˆ†ن¸ه€¼ه®ڑçگ†ï¼Œç¬¬ن؛”é¢کçں©éکµه¯¹è§’هŒ–,第ه…é¢کو¦‚çژ‡ه¯†ه؛¦ï¼Œه¤§é¢ک都ه¾ˆه¸¸è§„考点,ن¸ه€¼ه®ڑçگ†è؟™ن¸ھ考点较éڑ¾ï¼Œه‡؛é¢کçژ‡ن¸چé«ک,و²،وœ‰هڈ‚考و€§ï¼Œه…¶ه®ƒçڑ„都考وں¥è®،ç®—ن¸ژه…¬ه¼ڈم€‚
م€گو€»ç»“م€‘考试ه¤§éƒ¨هˆ†é¢کçڑ„çں¥è¯†ç‚¹ن¸ژه¾€ه¹´ه¹¶و— ه·®هˆ«ï¼Œهڈھوک¯ه› ن¸؛ه¤§é¢کçڑ„ه‡ڈه°‘,هœ¨ه‡؛é¢که½¢ه¼ڈن¸ٹهپڑن؛†و”¹هڈک,综هگˆو€§ه¢هٹ ,è®،ç®—é‡ڈه¢ه¤§ï¼Œéœ€è¦پو›´ه¥½هœ°çگ†è§£çں¥è¯†ç‚¹ï¼Œçپµو´»è؟گ用و€§è´¨ه’Œو¦‚ه؟µï¼Œهٹ ه؟«هپڑé¢کé€ںه؛¦ï¼Œçژ°هœ¨ه¤§é¢که‡؛é¢کéڑ¾ه؛¦éƒ½ن¸چه¤ھé«ک,ن¸چè؟‡è®،ç®—é‡ڈ都ن¸چه°ڈ,وڈگهچ‡هپڑé¢کé€ںه؛¦ï¼Œو‰“牢هں؛ç،€ï¼Œè€ƒè¯•ه¯¹çں¥è¯†ç‚¹è؟گ用و–¹é¢è؟›è،Œن؛†و›´و·±ه±‚و¬،çڑ„考وں¥ï¼Œو€»çڑ„و¥è¯´è€ƒç‚¹هں؛وœ¬éƒ½وک¯ه¸¸è€ƒç‚¹ï¼Œéœ€è¦پ细ه؟ƒن¸€ç‚¹ï¼ŒهگŒو—¶هں؛ç،€و›´ç‰¢ه›؛ن¸€ç‚¹ï¼Œè®،ç®—ن¸چه‡؛é”™م€‚
و¸©é¦¨وڈگç¤؛ï¼ڑو–‡ç« ç”±ن½œè€…233网و ،-chenjing独立هˆ›ن½œه®Œوˆگ,وœھç»ڈè‘—ن½œوƒن؛؛هگŒو„ڈç¦پو¢è½¬è½½م€‚
