(一)回归分析的概念
1„ÄÅÂõûÂΩíÂàÜÊûêÔºöÊåáÊÝπÊçÆÁõ∏ÂÖ≥ÂÖ≥Á≥ªÁöÑÂÖ∑‰ΩìÂΩ¢ÊÄÅÔºåÈÄâÊ㩉∏ĉ∏™ÂêàÈÄÇÁöÑÊï∞Â≠¶Ê®°ÂûãÔºåÊù•Ëø뉺ºÂú∞Ë°®ËææÂèòÈáèÈó¥Áöщæù˵ñÂÖ≥Á≥ª„ÄÇ
2„ÄÅÂõÝÂèòÈáèÔºöË¢´È¢ÑʵãÊàñË¢´ËߣÈáäÁöÑÂèòÈáèÔºå‰∏ÄËà¨Áî®YË°®Á§∫
3„ÄÅËá™ÂèòÈáèÔºöÁî®Êù•È¢ÑʵãÊàñËߣÈáäÂõÝÂèòÈáèÁöÑÂèòÈáèÔºå‰∏ÄËà¨Áî®XË°®Á§∫„ÄÇ
【单选题】选择合适的统计模型从一个变量的变化来推测另一个变量的变化情况,适用的统计方法是( )。
A、散点图
B、移动平均
C、相关系数
D、回归分析
(二)一元线性回归模型
ÊÝπÊçÆËá™ÂèòÈáèÁöѧöÂ∞ëÂà܉∏∫Ôºö‰∏ÄÂÖÉÂõûÂΩíÊ®°ÂûãÂíå§öÂÖÉÂõûÂΩíÊ®°Âûã„ÄÇ
ÊÝπÊçÆÊòØÂê¶ÊòØÁ∫øÊÄßÂà܉∏∫ÔºöÁ∫øÊÄßÂõûÂΩíÊ®°ÂûãÂíåÈùûÁ∫øÊÄßÂõûÂΩíÊ®°Âûã„ÄÇ
1„Äʼn∏ÄÂÖÉÁ∫øÊÄßÂõûÂΩíÊ®°ÂûãÔºöÊèèËø∞‰∏§‰∏™ÂèòÈáè‰πãÈó¥Áõ∏ÂÖ≥ÂÖ≥Á≥ªÁöÑÊúÄÁÆÄÂçïÁöÑÂõûÂΩíÊ®°Âûã„ÄÇÂõûÂΩíÊ®°ÂûãÂè؉ª•Áî®ÊèèËø∞ÂõÝÂèòÈáèY¶ljΩï‰æù˵ñËá™ÂèòÈáèXÂíåËØØÂ∑ÆÈ°πŒµÁöÑÊñπÁ®ãÊù•Ë°®Á§∫„ÄÇ
2、只涉及一个自变量的一元线性回归模型可以表示为:Y=β0+β1X+ε
β0、β1——模型的参数。
(1)YÊòØXÁöÑÁ∫øÊÄßÂáΩÊï∞(Œ≤0+Œ≤1X)Âä݉∏äËØØÂ∑ÆÈ°πŒµ„ÄÇ
(2)Œ≤0+Œ≤1XÂèçÊò݉∫ÜÁ∫éXÁöÑÂèòÂåñËÄåºï˵∑ÁöÑYÁöÑÁ∫øÊÄßÂèòÂåñ„ÄÇ
(3)ËØØÂ∑ÆÈ°πŒµÊò؉∏™ÈöèÊú∫ÂèòÈáèÔºåÂèçÊò݉∫ÜÈô§XÂíåY‰πãÈó¥ÁöÑÁ∫øÊÄßÂÖ≥Á≥ª‰πã§ñÁöÑÈöèÊú∫ÂõÝÁ¥ÝÂØπYÁöÑÂΩ±ÂìçÔºåÊò؉∏çËÉΩÁî±XÂíåY‰πãÈó¥ÁöÑÁ∫øÊÄßÂÖ≥Á≥ªÊâÄËߣÈáäÁöÑYÁöÑÂèòºÇÊÄß„ÄÇ
3„ÄÅÊèèËø∞ÂõÝÂèòÈáèYÁöÑÊúüÊúõE(Y)¶ljΩï‰æù˵ñËá™ÂèòÈáèXÁöÑÊñπÁ®ãÁß∞‰∏∫ÂõûÂΩíÊñπÁ®ã„Älj∏ÄÂÖÉÁ∫øÊÄßÂõûÂΩíÊñπÁ®ãÁöÑÂΩ¢Âºè‰∏∫ÔºöE(Y)=Œ≤0+Œ≤1X
一元线性回归方程的图示是一条直线,β0是回归直线的截距,β1是回归直线的斜率,表示X每变动一个单位时,E(Y)的变动量。
1、估计回归方程:
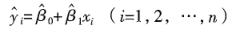
2„ÄÅÂéüÁêÜÔºöÊúÄÂ∞è‰∫å‰πòÊ≥ïÂ∞±Êò؉ΩøÂæóÂõÝÂèòÈáèÁöÑËßÇʵãÂĺyi‰∏鉺∞ËÆ°Âĺ≈∑iÔºå‰πãÈó¥ÁöÑÁ¶ªÂ∑Æ(ÂèàÁß∞ÊÆãÂ∑Æ)Âπ≥ÊñπÂíåÊúÄÂ∞èÊù•‰º∞ËÆ°ÂèÇÊï∞Œ≤0ÔºåÂíå Œ≤1ÔºåÁöÑÊñπÊ≥ï„ÄÇ
【单选题】在回归分析中,估计回归系数的最小二乘法的原理是( )
A„ÄʼnΩøÂæóÂõÝÂèòÈáèËßÇʵãÂĺ‰∏éÂùáÂĺ‰πãÈó¥ÁöÑÁ¶ªÂ∑ÆÂπ≥ÊñπÂíåÊúÄÂ∞è
B„ÄʼnΩøÂæóÂõÝÂèòÈá艺∞ËÆ°Âĺ‰∏éÂùáÂĺ‰πãÈó¥ÁöÑÁ¶ªÂ∑ÆÂπ≥ÊñπÂíåÊúÄÂ∞è
C、使得观测值与估计值之间的乘积最小
D„ÄʼnΩøÂæóÂõÝÂèòÈáèËßÇʵãÂĺ‰∏鉺∞ËÆ°Âĺ‰πãÈó¥ÁöÑÁ¶ªÂ∑ÆÂπ≥ÊñπÂíåÊúÄÂ∞è
(一)回归模型的拟合效果分析
1、模型的检验
一般情况下,在使用估计的回归方程之前,需要对模型进行检验:
‚ëÝÁªìÂêàÁªèʵéÁêÜËÆ∫ÂíåÁªèÈ™åÂàÜÊûêÂõûÂΩíÁ≥ªÊï∞ÁöÑÁªèʵéÂê´‰πâÊòØÂê¶ÂêàÁêÜ;
②分析估计的模型对数据的拟合效果如何;
③对模型进行假设检验。
2„ÄÅÂÜ≥ÂÆöÁ≥ªÊï∞R2Ôºö‰πüÁß∞‰∏∫ÊãüÂêà‰ºòÂ∫¶ÊàñÂà§ÂÆöÁ≥ªÊï∞ÔºåÂè؉ª•ÊµãÂ∫¶ÂõûÂΩíÊ®°ÂûãÂØπÊÝ∑Êú¨Êï∞ÊçÆÁöÑÊãüÂêàÁ®ãÂ∫¶„ÄÇ
ÂÜ≥ÂÆöÁ≥ªÊï∞ÊòØÂõûÂΩíÊ®°ÂûãÊâÄËÉΩËߣÈáäÁöÑÂõÝÂèòÈáèÂèòÂåñÂçÝÂõÝÂèòÈáèÊĪÂèòÂåñÁöÑÊØî‰æãÔºåÂèñÂĺËåÉÂõ¥‰∏∫[0Ôºå1]
(1)ÂÜ≥ÂÆöÁ≥ªÊï∞Ë∂äÈ´òÔºåÊ®°ÂûãÁöÑÊãüÂêàÊïàÊûúÂ∞±Ë∂ä•ΩÔºåÂç≥Ê®°ÂûãËߣÈáäÂõÝÂèòÈáèÁöÑËÉΩÂäõË∂äº∫„ÄÇ
¶ÇÊûúÊâÄÊúâËßÇʵãÁÇπÈÉΩËêΩÂú®ÂõûÂΩíÁõ¥Á∫ø‰∏äÔºåR2=1ÔºåËØ¥ÊòéÂõûÂΩíÁõ¥Á∫øÂè؉ª•ËߣÈáäÂõÝÂèòÈáèÁöÑÊâÄÊúâÂèòÂåñ„ÄÇ
R2=0ÔºåËØ¥ÊòéÂõûÂΩíÁõ¥Á∫øÊóÝÊ≥ïËߣÈáäÂõÝÂèòÈáèÁöÑÂèòÂåñÔºåÂõÝÂèòÈáèÁöÑÂèòÂåñ‰∏éËá™ÂèòÈáèÊóÝÂÖ≥„ÄÇ
(2)现实应用中R2大多落在0和1之间,R2越接近于1,回归模型的拟合效果越好;R2越接近于0,回归模型的拟合效果越差。
2、回归系数的显著性检验
Âú®Â§ßÊÝ∑Êú¨ÂÅáÂÆöÁöÑÊù°‰ª∂‰∏ãÔºåÂõûÂΩíÁ≥ªÊï∞ÁöÑÊúÄÂ∞è‰∫å‰πò‰º∞ËÆ°Èáè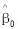 Âíå
Âíå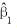 ÔºåÊ∏êËøõÊú牪éÊ≠£ÊÄÅÂàÜÂ∏ÉÔºåÂè؉ª•Áî®tÊ£ÄÈ™åÊñπÊ≥ïÈ™åËØÅËá™ÂèòÈáèXÂØπÂõÝÂèòÈáèYÊòØÂê¶ÊúâÊòæËëóÂΩ±Âìç„ÄÇ
ÔºåÊ∏êËøõÊú牪éÊ≠£ÊÄÅÂàÜÂ∏ÉÔºåÂè؉ª•Áî®tÊ£ÄÈ™åÊñπÊ≥ïÈ™åËØÅËá™ÂèòÈáèXÂØπÂõÝÂèòÈáèYÊòØÂê¶ÊúâÊòæËëóÂΩ±Âìç„ÄÇ
tÊ£ÄÈ™åÁöÑÂéüÁêÜÊòØÂèçËØÅÊ≥ïÔºöÂú®ÂéüÂÅáËÆæ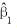 =0(Ëá™ÂèòÈáèXÂØπÂõÝÂèòÈáèYÊ≤°ÊúâÂΩ±Âìç)Ê≠£Á°ÆÁöÑÂÅáËÆæ‰∏ãÔºåÂü∫‰∫é
=0(Ëá™ÂèòÈáèXÂØπÂõÝÂèòÈáèYÊ≤°ÊúâÂΩ±Âìç)Ê≠£Á°ÆÁöÑÂÅáËÆæ‰∏ãÔºåÂü∫‰∫é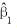
ÁöÑÊäΩÊÝ∑ÂàÜÂ∏ÉËÆ°ÁÆó‰∏Äʨ°ÊäΩÊÝ∑ÊÉÖÂܵ‰∏ãÂæóÂà∞ËØ•ÊÝ∑Êú¨ÊàñÊõ¥ÊûÅÁ´ØÊÝ∑Êú¨ÁöÑʶÇÁéá(PÂĺ)Ôºå¶ÇÊûúP<0.05ÔºåÂàôÂè؉ª•Âú®0.05ÁöÑÊòæËëóÊÄßÊ∞¥Âπ≥‰∏ãÊãíÁªùÂéüÂÅáËÆæÔºåËƧ‰∏∫Ëá™ÂèòÈáèXÂØπÂõÝÂèòÈáèYÊúâÊòæËëóÊÄßÂΩ±ÂìçÔºåÂç≥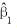 ‚âÝ0„ÄÇ
‚âÝ0„ÄÇ
【单选题】回归系数检验的目的是( )
A、测算回归模型的拟合效果
B、估计回归系数的大小
C、检验自变量的经济含义是否正确
D„ÄÅÊ£ÄÈ™åËá™ÂèòÈáèÂØπÂõÝÂèòÈáèÊòØÂê¶ÊúâÊòæËëóÂΩ±Âìç
(二)模型预测
ÂõûÂΩíÂàÜÊûêÁöщ∏ĉ∏™Èáç˶ÅÂ∫îÁî®Â∞±ÊòØÈ¢ÑʵãÔºåÂç≥Âà©Áº∞ËÆ°ÁöÑÂõûÂΩíÊ®°ÂûãȢщº∞ÂõÝÂèòÈáèÊï∞Âĺ„ÄÇ
(三)二元回归模型案例
§öÂÖÉÂõûÂΩíÊ®°ÂûãÂú®ÂÆûÈôÖÂ∫îÁ∏≠ÔºåÈöèÁùÄËá™ÂèòÈáè‰∏™Êï∞ÁöÑ¢ûÂäÝÔºåÂç≥‰ΩøÂú®Êúâ‰∫õËá™ÂèòÈáè‰∏éÂõÝÂèòÈáèÂÆåÂÖ®‰∏çÁõ∏ÂÖ≥ÁöÑÊÉÖÂܵ‰∏ãÔºåÂÜ≥ÂÆöÁ≥ªÊï∞R2‰πü‰ºö¢û§߄Älj∏∫ÈÅøÂÖçÂõÝ¢ûÂäÝËá™ÂèòÈáè‰∏™Êï∞ËÄåÈ´ò‰º∞ÊãüÂêàÊïàÊûúÁöÑÊÉÖÂܵԺå§öÂÖÉÂõûÂΩíÊ®°Âûã‰∏ÄËਉΩøÁøÆÊ≠£‰∫ÜËá™Áî±Â∫¶ÁöÑË∞ÉÊï¥ÂêéR2(Adjusted R Square)„ÄÇË∞ÉÊï¥ÂêéR2ËÄÉËôë‰∫ÜËá™ÂèòÈáè‰∏™Êï∞¢ûÂäÝÂ∏¶Êù•ÁöÑÂΩ±ÂìçÔºåÂú®Êï∞Âĺ‰∏äÂ∞è‰∫éR2„ÄÇ
【多选题】关于回归模型决定系数(R2)的说法,正确的有( )
A、R2越接近0,回归模型的拟合效果越差
B„ÄÅR2ÊòØÂõûÂΩíÊ®°ÂûãÊâÄËÉΩËߣÈáäÁöÑÂõÝÂèòÈáèÂèòÂåñÂçÝÂõÝÂèòÈáèÊĪÂèòÂåñÁöÑÊØî‰æã
C、R2数值越大,回归模型的拟合效果越好
D、R2的取值范围是>0
E、自变量个数对R2没有影响
Ê∏©È¶®ÊèêÁ§∫ÔºöÊñáÁ´ÝÁΩúËÄÖ233ÁΩëÊÝ°-lxhÁã¨Á´ãÂàõ‰ΩúÂÆåÊàêÔºåÊú™ÁªèËëó‰ΩúÊùɉ∫∫ÂêåÊÑèÁ¶ÅÊ≠¢ËΩ¨ËΩΩ„ÄÇ